Se entiende por árbol al grafo G=<V,A> que cumple con las propiedades de ser simple, conexo y sin ciclos.
Otra definición equivalente sería:
Un árbol es un grafo simple no dirigido G que satisface:
- G es conexo y no tiene ciclos .
- G no tiene ciclos y, si se añade alguna arista se forma un ciclo.
- G es conexo y si se le quita alguna arista deja de ser conexo.
- G es conexo y el grafo completo de 3 vértices no es un menor de G.
- Dos vértices cualquiera de G están conectados por un único camino simple.
Las condiciones anteriores son todas equivalentes, es decir, si se cumple una de ellas otras también se cumplen. Para árboles finitos además se cumple que: Si un árbol G tiene un número finito de vértices, n, entonces tiene n − 1 aristas. (3)
O la siguiente de carácter constructiva:
Un árbol es un grafo G definido recursivamente por las siguientes proposiciones:
- Un árbol es un solo nodo.
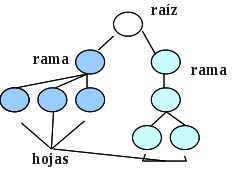
- Un árbol es un nodo conectado mediante sendas aristas a varios árboles denominados ramas.
Normalmente se identifica a un vértice como raíz o padre de la cual deriva aristas a otros nodos que se llaman hijos de dicho padre o raíz. A los nodos que no tienen descendencia se les llama hojas. (1)
Estructura de árbol con su tipo base T
 |
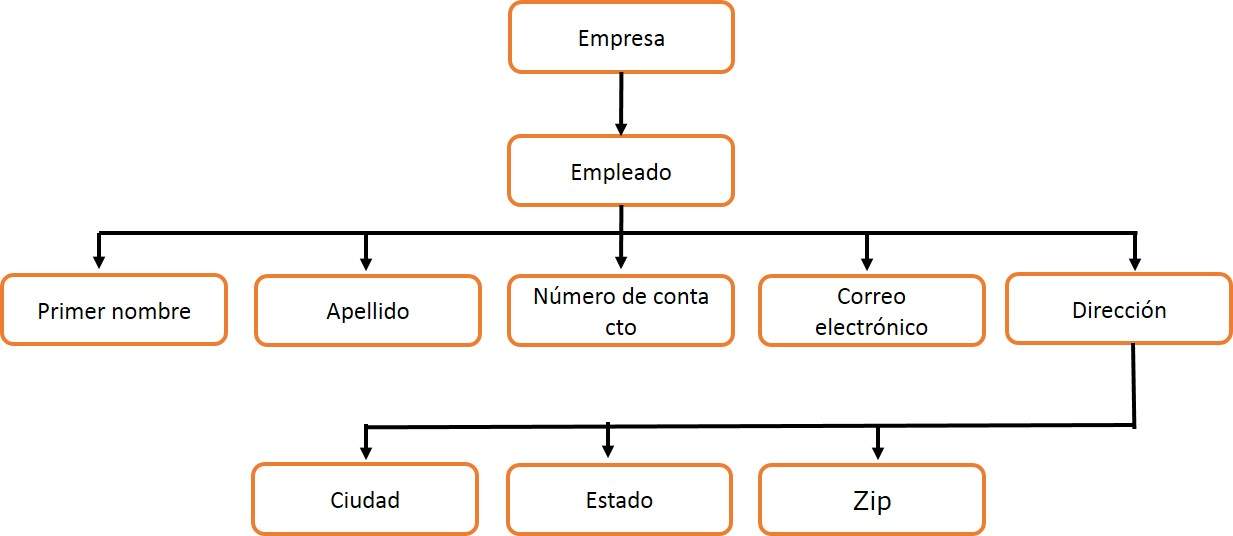
| Representación de una estructura de árbol: a) conjuntos anidados; b) paréntesis anidados; c) sangría (escalonamiento); d) gráfica |
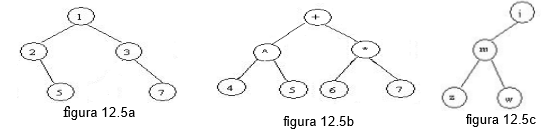
Un arbol ordenado es un árbol en el cual las ramas de cada nodo están ordenadas. En consecuencias, los dos árboles ordenados de la siguiente figura son objetos diferentes:
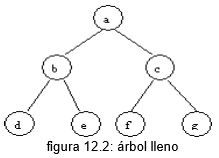
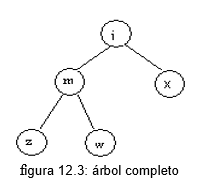
Un nodo y que está directamente debajo del nodo x se denomina descendiente (directo) de x si x está en el nivel i, entonces que dice que y es un nivel i + i. A la inversa, se dice que el nodo x es el ancestro (directo) de y. La raíz de un árbol se define como localizada en el nivel 0. Se dice que el nivel máximo de cualquier elemento de un árbol es su profunidad o altura.
Si un elemento no tiene descendientes, se le denomina nodo terminal o bien hoja, y un elemento que no es temrinal es un nodo interior. El número de descendientes (directos) de un nodo interior se conoce como su grado. El grado máximo en todos los nodos es el grado de un árbol. El número de ramas o aristas que tienen que ser recorridas a fin de proceder desde la raíz hasta un nodo x se llama longitud de trayectoria de x. La raíz tiene una longitud de trayectoria 0, sus descendientes directos tienen una longitud de trayectoria 1, etcétera. En general, un nodo en el nivel i tiene la longitud de trayectoria i. La longitud de trayectoria de un árbol se define como la suma de las longitudes de trayectoria de todas sus componentes. También se le denomina su longitud de trayectoria interna. (2)